Neural Networks

Neural Networks are the most popular family of Machine Learning algorithms. They are so popular that there is an entire field dedicated to the use of "deep" neural networks called deep learning. The depth of a neural network is characterized by the number of layers. The simplest type of neural network is the Feed Forward Neural Network.

Feed Forward Neural Network

Neural networks can be created by assembling several smaller models into a connected network. The feedforward neural network is very straightforward: information only moves in the forward direction.

Each layer in the neural network is made up of individual units. These individual units are typically Perceptrons, which is a binary classification algorithm. Broadly speaking, a neural network is made up of an input layer followed by zero or more hidden layer(s) and concluded with an output layer.

The input layer receives the represented data and passes the information to the hidden layer(s). The hidden layer(s) processes the input and passes the distilled information to the next hidden layer until it reaches the output layer. Neural networks used for classification will have as many units in the output layer as the number of classes. Each of these units correspond to a specific class and their values correspond to a confidence score for that class. The class with the highest score is the inferred class. To use a neural network for regression, the last layer would have one unit whose value becomes the regression output.

Layers are connected through their units. In a fully connected neural network, each unit is connected to all of the units in the next layer. The diagram above represents a fully connected neural network. The connections can also be pooled, where multiple units are connected to a single unit in the next layer.

The parameters in a neural network are typically referred to as weights, which is determined through the training process. Every connection contains a corresponding weight value, this value determines how important that connection is. Suppose we have units \(X_1\) and \(X_2\) connected to unit \(Y\). The outputs of \(X_1\) and \(X_2\) are \(x_1\) and \(x_2\). To calculate the output of \(Y\), denoted \(y\), we take the weighted sum (plus the bias parameter if applicable) \(w_1 x_1 + w_2 x_2 + bias\) as the input. This input is passed to a non-linear Activation Function to produce \(y\).

Activation Functions

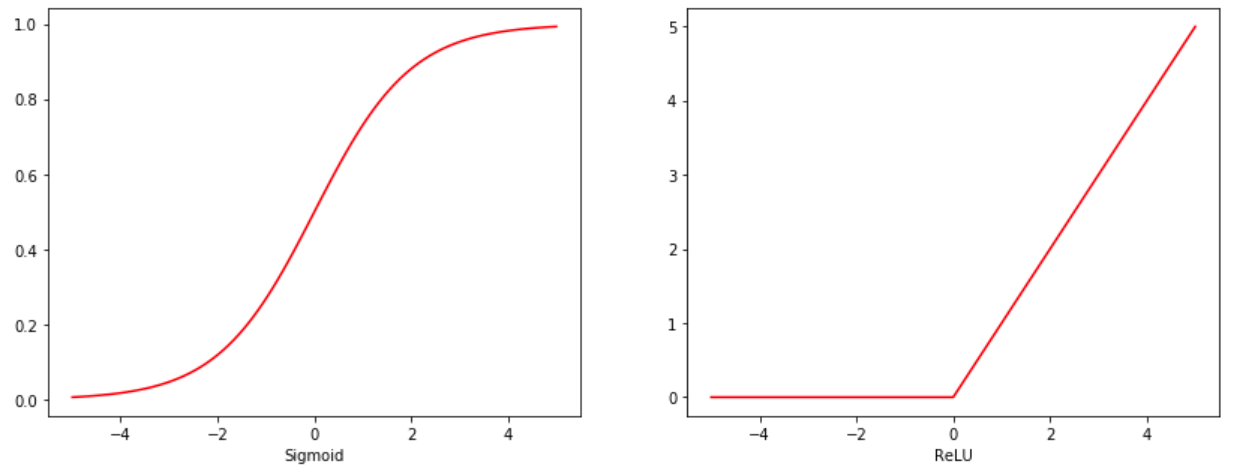
The Rectifier is one of the most popular activation functions. A unit using this function is known as a rectified linear unit (ReLU). The ReLU function takes the maximum between 0 and the input:

$$f(x) = max(0, x)$$

The Softmax function is typically used as the activation function in the last layer for classification. The outputs from this function is a probablistic representation of Euler's constant raised to the power of the input. The range is between 0 and 1.

$$softmax(x)_i = \frac{e^{x_i}}{\sum_{j}^{ }e^{x_j}}$$

The Sigmoid function is the softmax function with two classes. If this function looks familiar, it's because it's the same function used to isolate probability for logistic regression (can you show the derivation?).

$$sigmoid(x) = \frac{e^{x_1}}{e^{x_1} + e^{x_2}}$$

How are the weights in a Neural Network determined?

There are several algorithms that we can use to find the optimal weights. One of these approaches is known as backpropagation. The motivating idea behind this algorithm is that we want to minimize the error of the prediction (represented by a predetermined loss function). On a very high level, we start by choosing some randomized weights.

Then we repeat these steps until some convergence criteria is met:

The most common convergence criteria is to keep repeating these steps until we reach a certain number of epochs. Each epoch represents one iteration of the entire training data through this algorithm.

Beyond Tabular Data

One of the most popular applications of feedforward neural networks are Convolutional Neural Networks which is well suited for modeling spatial data such as images. Images are partitioned by their color channels (grayscale images only have one channel) where each color channel is represented by an array with values indicating the hue of each pixel.

In addition to feedforward neural networks, we also have Recurrent Neural Networks which is well suited to learn from sequential data. In a recurrent neural network, the connections between units form a directed graph where cycles can be created through the connections. These networks are suitable for modeling language, where the order of words matter.